一、导通模式基础原理
1.1 CCM/DCM模式判据

| 特征维度 | CCM模式 | DCM模式 |
|---|---|---|
| 判断条件 | 电感电流连续不归零 | 电感电流在一个周期内有归零时间 |
| 电流波形特征 | 三角波连续无零区 | 三角波+零电流平台 |
| 应用场景 | 大功率/低纹波要求 | 轻载/小功率/快速响应应用 |
1.2 对比分析表
| 对比维度 | 非同步整流 | 同步整流 |
|---|---|---|
| 续流元件 | 快恢复二极管/肖特基二极管 | MOSFET(其体二极管在死区时工作) |
| 导通损耗 | 正向压降×电流 $$V_F \cdot I$$ | 导通电阻×电流² $$I^2 \cdot R_{ds(on)}$$ |
| 驱动复杂度 | 无需控制 | 需互补PWM+死区控制 |
| 反向恢复问题 | 存在反向恢复损耗 | 体二极管存在反向恢复损耗(主要在死区时间产生) |
1.3 模式判定与临界点
在既定的电路参数($V_{in}, V_{out}, f_{sw}, L$)下,电感纹波电流峰峰值 $\Delta I_L$ 是固定的。此时,DCDC工作在何种模式,完全取决于负载电流 $I_{out}$ 的大小。
判定逻辑: 电感电流可以看作是一个叠加在直流分量上的三角波。
- 直流分量:等于负载电流 $I_{out}$。
- 交流分量:等于纹波电流 $\Delta I_L$(由电感量决定)。
| 负载状态 | 判据公式 | 工作模式 | 物理现象 |
|---|---|---|---|
| 重载 | $I_{out} > \frac{1}{2}\Delta I_L$ | CCM | 电流三角波谷底高于0A,电感持续放电。 |
| 临界 | $I_{out} = \frac{1}{2}\Delta I_L$ | BCM | 电流三角波谷底刚好触碰0A。 |
| 轻载 | $I_{out} < \frac{1}{2}\Delta I_L$ | DCM | 电流三角波“试图”变为负值,被二极管阻断(断流),电流归零。 |
结论:对于非同步的电路,负载电流减小到一定程度(临界电流),电路会自动滑入DCM模式。
1.4 工程设计准则与FCCM
虽然轻载会进入DCM,但在工程设计电感时,必须基于CCM模式进行计算。
1.4.1 黄金设计法则
为了兼顾纹波大小、电感体积和动态响应,行业内设计电感时遵循纹波率 $r$ 准则:
$$
r = \frac{\Delta I_L}{I_{out_max}} \approx 0.2 \sim 0.4
$$
设计含义:
- 我们设定在满载时,纹波占直流电流的 30% 左右。
- 这意味着:只要负载电流大于满载的 15%(即 $0.3/2$),电路就会进入CCM模式。
- 为何不按DCM设计? 若按DCM设计(允许满载即DCM),会导致纹波电流极大,造成输出电容过热、磁芯饱和及电压纹波超标。
1.4.2 同步整流的特殊情况:FCCM
对于采用MOSFET作为下管的同步整流芯片(如SC8701/SC8815),存在两种可选的工作逻辑:
- 二极管仿真模式:
- 行为:模拟二极管特性,检测到电感电流归零时关闭下管MOS。
- 结果:轻载自动进入DCM,效率高,适合电池供电应用。
- 强制连续模式:
- 行为:无论负载多轻,MOSFET均按照互补PWM工作,允许电流倒灌(从输出端流回输入端)。
- 结果:永远处于CCM(即使空载,电流呈正负交替的三角波)。
- 优势:频率固定(利于EMI滤波),动态响应极快。
- 缺点:轻载效率极低(由于无功环流损耗)。
1.5 纹波深度解析:电感、电压与电容
在电源设计中,纹波不仅是波形的“毛刺”,更是决定效率、体积和寿命的底层变量。我们将纹波分为三个维度进行深度剖析。
1.5.1 电感纹波电流 ($\Delta I_L$):磁芯的负担
1. 什么是电感纹波电流? 在开关电源中,电感两端的电压是高频切换的,这导致流过电感的电流不是一条平直的直线,而是一个三角波。
- 上升阶段:开关管导通,电流线性上升,电感充能。
- 下降阶段:开关管关断,电流线性下降,电感放能。
- 这个三角波的峰值与谷值之差,就是电感纹波电流 ($\Delta I_L$)。它叠加在直流负载电流之上,是导致电感发热的主要原因。
2. 设定较大纹波电流(即选用小电感 L)的权衡 当我们将纹波率设计得较大(例如 >40%),意味着选用了感值较小的电感。
- 带来的优势:
- 动态响应极快:这是小电感最大的杀手锏。电感本质是阻碍电流变化的元件,感值越小,对电流变化的阻碍越小。当负载突然跳变(如CPU从休眠到满载)时,小电感能以极高的压摆率拉升电流,减少输出电压的跌落幅度。
- 体积与成本红利:实现小感值通常需要更少的线圈匝数。这直接导致直流电阻(DCR)降低,减少了铜损。同时,更少的匝数允许使用更小的磁芯骨架,从而减小了电源的整体体积和BOM成本。
- 无功环流小:在同样的直流负载下,小感值虽然纹波大,但如果是DCM模式,其实际储能周期短。
- 引发的代价:
- 磁芯损耗(铁损)剧增:这是最致命的副作用。纹波幅度大,意味着磁芯内部的磁通密度摆幅($\Delta B$)巨大。根据施泰因梅茨公式,磁芯损耗与磁通摆幅的指数次方成正比。这会导致电感在重载甚至轻载时都严重发烫。
- 更容易饱和:峰值电流 $I_{peak} = I_{DC} + 0.5 \Delta I_L$。纹波越大,叠加在直流上的峰值就越高,使得磁芯更容易触碰到饱和磁感应强度($B_{sat}$)。
- 加重电容负担:巨大的交流纹波电流会毫无保留地流入输出电容,导致输出电压纹波难以控制,且让电容过热。
3. 设定较小纹波电流(即选用大电感 L)的权衡 当我们将纹波率设计得非常小(例如 <20%),意味着选用了感值很大的电感。
- 带来的优势:
- 磁芯“冷静”:磁通摆幅极小,铁损几乎可以忽略不计,非常适合对温升要求严苛的场合。
- 输出电压纯净:流向输出电容的交流分量很少,使得输出电压纹波天然就很低,对后级滤波电容的要求大幅降低。
- 开关管RMS电流低:流过MOSFET的有效电流更接近直流平均值,导通损耗($I^2R$)略有降低。
- 引发的代价:
- 动态响应迟钝:大电感像一个巨大的飞轮,极难加速也极难减速。当负载突变时,电流跟不上需求,只能靠透支输出电容的电荷来维持电压,导致输出电压出现巨大的跌落或过冲。
- 体积与铜损双高:为了获得大感值且不饱和,必须增加匝数或使用更大的磁芯。多匝数直接导致直流电阻(DCR)显著增加,在大电流输出时,线圈的铜损会超过磁芯的铁损,成为发热主因。
1.5.2 输出纹波电压 ($\Delta V_{out}$):负载的干扰
1. 什么是输出纹波电压? 这是指在理想的直流输出电压上,叠加的一层微小交流波动。简单来说,就是输出电压“不干净”的程度。
- 成因:上述的电感纹波电流(三角波)必须流经输出电容回到地。当电流流过电容时,会在电容的内部阻抗上产生压降,这个压降就是纹波电压。
- 重要性:如果纹波电压过大,会导致后级敏感电路(如音频放大器、ADC)出现噪声干扰或误动作。
2. 公式拆解与主导因素 纹波电压主要由两部分构成:
$$
\Delta V_{out} \approx \Delta V_{ESR} + \Delta V_{Cap} = \Delta I_L \cdot ESR + \frac{\Delta I_L}{8 \cdot C_{out} \cdot f_{sw}}
$$
- 第一类:电阻主导型(如铝电解电容、钽电容) 对于传统的铝电解电容,其等效串联电阻 (ESR) 通常在几十毫欧到几百毫欧。此时,公式中的第一项 $\Delta I_L \cdot ESR$ 占据绝对主导地位,电容容量本身的影响微乎其微。
- 现象:纹波波形与电感电流波形几乎完全一样,是尖锐的三角波。
- 对策:单纯增加容量(例如从 470uF 换到 1000uF)往往效果不明显,因为同一系列的电容 ESR 变化不大。最有效的手段是选择“Low ESR”系列电容,或者采用多颗小容量电容并联,以降低总 ESR。
- 第二类:电容主导型(如 MLCC 陶瓷电容) 陶瓷电容的 ESR 极低(通常 <5mΩ),此时电阻产生的纹波几乎为零,纹波主要由电容充放电积累的电荷决定。
- 现象:纹波波形是电流的积分,呈现平滑的弧形。
- 对策:在此场景下,增加容量 $C$ 或提高开关频率 $f_{sw}$ 是降低纹波的直接手段。
1.5.3 电容纹波电流 ($I_{RMS}$):隐形的寿命杀手
这是电源设计中最凶险的参数。不同于电感发热(通常只是效率低),电容过热会导致物理失效——电解液汽化、密封圈爆裂或陶瓷介质热击穿。
为什么关注 RMS (有效值)? 电容发热遵循焦耳定律 $P = I_{RMS}^2 \cdot ESR$。必须注意,这里的 $I$ 不是直流负载电流,而是流进流出电容的交流分量。
拓扑结构的决定性影响:
- 最恶劣工况:Buck 的输入端 & Boost 的输出端 在这两个位置,电容承受的是断续的脉冲电流。
- 以 Buck 的输入电容为例:上管导通时,电流瞬间从 0 跳变到 10A;上管关断时,瞬间跌回 0。这种剧烈的矩形波跳变含有极其丰富的高频谐波,且有效值极高(约为输出电流的一半)。
- 后果:如果是普通的铝电解电容,在大电流 Buck 的输入端会迅速发烫鼓包。
- 对策:必须在这些位置使用高分子固态电容(具备极高纹波耐受力)或多颗 MLCC 并联。严禁单颗普通电解电容“裸奔”。
- 相对温和工况:Buck 的输出端 & Boost 的输入端 在这两个位置,电容面对的是电感,电流是连续的三角波。
- 虽然也有纹波,但电流没有剧烈的突变,RMS 值相对较小(仅为纹波电流 $\Delta I_L$ 的 $1/\sqrt{12}$)。
- 对策:这里的电容主要压力在于维持电压稳定(ESR要求),而非生存压力(发热要求)。
二、自举电路
2.1 核心原因
VS浮动引发的VGS失控
N-MOSFET需要满足以下条件才能导通。对于上管,其源极S的电位($V_S$)是浮动的,导致需要一个浮动的驱动电压来维持稳定的$V_{GS}$。
$$V_{GS} > V_{th}$$
理想驱动条件:
$$
V_{GS} = V_G – V_S > V_{th}
$$
在开关过程中$V_S$剧烈跳变(如BUCK模式下$V_S$在$V_{IN}$与GND间切换)。若驱动电压$V_G$不跟随$V_S$抬升,则$V_{GS}$会失效。
失效机理:
- 导通阶段:
$$
V_S \approx V_{IN} \Rightarrow V_{GS} = V_G – V_{IN}
$$
若驱动电压$V_G$未抬升(例如仍为$V_{CC}$)$\Rightarrow$ $V_{GS}$可能小于阈值电压$V_{th}$ $\Rightarrow$ MOSFET无法完全导通,损耗剧增。 - 关断阶段:
$$
\frac{dV_S}{dt} \ \text{通过米勒电容} \ C_{gd} \ \text{耦合} \ \Rightarrow V_{GS} \ \text{产生尖峰} \ \Rightarrow \text{误导通风险}
$$
2.2 自举电容的工作机制
由于上管源极 $V_S$ 的电位是不固定的,外部固定的电源(如 $V_{CC}=12V$)无法直接用来驱动上管。自举电容 $C_{boot}$ 在此充当了一个“浮动电池”的角色,其工作循环分为“充电”与“供电”两个阶段:
1. 充电阶段(下管导通,能量补充)
- 状态:当下管导通(或下管体二极管续流)时,上管源极电位被拉低至地:$V_S \approx 0V$。
- 动作:此时驱动电源 $V_{CC}$ 通过自举二极管($D_{boot}$)向自举电容($C_{boot}$)充电。
- 结果:电容两端电压被充至接近电源电压: $$ V_{C_{boot}} = V_{CC} – V_{F(Diode)}$$ 此时,电容就是一个储备好能量的“电池”。
2. 升压/供电阶段(上管导通,电压抬升)
- 状态:当驱动信号命令上管导通时,$V_S$ 迅速上升至输入电压 $V_{IN}$(例如 48V)。
- 动作:由于电容两端电压不能突变,电容正极(即上管驱动供电端 $V_B$)的电位会被强制“顶”起来,叠加在 $V_S$ 之上。
- 结果: $$ V_B = V_S + V_{C_{boot}} \approx V_{IN} + V_{CC}$$ 关键点:此时 $D_{boot}$ 反向截止,防止高压倒灌回 $V_{CC}$。驱动电路利用 $C_{boot}$ 储存的电荷,在 $V_G$ 和 $V_S$ 之间维持一个恒定的压差 $V_{GS} \approx V_{CC}$,确保上管在 $V_S$ 很高时依然能维持导通。
3. 占空比限制(电荷泄漏与刷新)
- 问题:$C_{boot}$ 的电荷是有限的。在上管导通期间,驱动电路的静态电流、MOSFET的栅极漏电流等会不断消耗电容的电荷,导致电压下降。
- 限制:如果上管长时间导通(即100%占空比),电容电荷耗尽,$V_{GS}$ 跌落至 $V_{th}$ 以下,上管将因进入线性区而烧毁。
- 结论:使用自举电路通常不能实现100%占空比,必须强制周期性地关断上管、开通下管,让 $V_S$ 回到 $0V$ 给电容“补电”。
三、同步Buck电路解析
3.1 拓扑结构
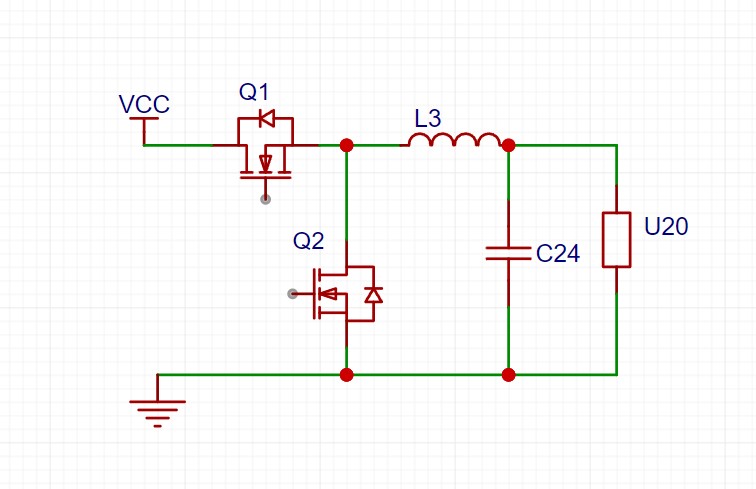
3.2 电压转换特性
CCM模式:
$$
\frac{V_{out}}{V_{in}} = D \quad (0 < D < 1)
$$
DCM模式:
$$
\frac{V_{out}}{V_{in}} = \frac{2}{1 + \sqrt{1 + \frac{4K}{D^2}}} \quad \left(K=\frac{2L}{R T_{sw}}\right)
$$
3.3 电感参数
CCM最小电感:
$$
L_{min} = \frac{(V_{in,max}-V_{out}) \cdot V_{out}}{V_{in,max} \cdot \Delta I_L \cdot f_{sw}}
$$
$$
(\Delta I_L \text{通常取最大额定输出电流} I_{out,max} \text{的20\%–40\%})
$$
实际电感范围推荐:
$$
1.2 \cdot L_{min} < L_{actual} < 1.8 \cdot L_{min}
$$
DCM临界条件 (BCM):
$$
L_{crit} = \frac{R(1-D)T_{sw}}{2} = \frac{V_{out}(1-D)}{2f_{sw}I_{out}}
$$
3.4 电流路径
| 工作阶段 | 开关状态 | 电流路径 |
|---|---|---|
| 储能阶段 | Q1导通, Q2关断 | Vin → Q1 → 电感 → (电容+负载) → GND |
| 续流阶段 | Q1关断, Q2导通 | GND → Q2 → 电感 → (电容+负载) → GND |
| DCM停滞阶段 | Q1关断, Q2关断 | 输出电容 → 负载 → GND |
四、同步Boost电路解析
4.1 拓扑结构
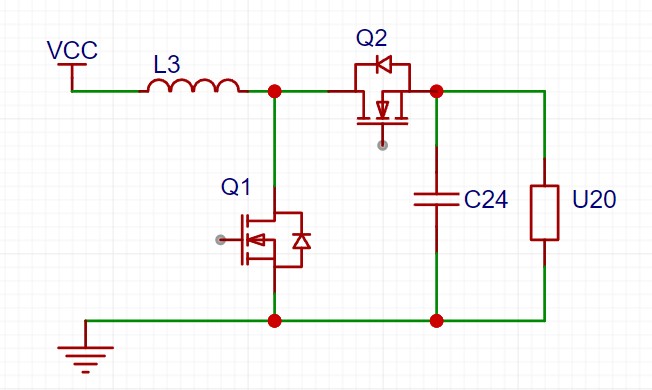
4.2 电压转换特性
CCM模式:
$$
\frac{V_{out}}{V_{in}} = \frac{1}{1-D} \quad (\text{实际D<0.85以保证控制})
$$
DCM模式:
$$
\frac{V_{out}}{V_{in}} = \frac{1+\sqrt{1+\frac{4D^2}{K}}}{2} \quad \left(K=\frac{2L}{R T_{sw}}\right)
$$
4.3 电感参数
CCM最小电感:
$$
L_{min} = \frac{V_{in}D}{\Delta I_L \cdot f_{sw}}
$$
$$
(\Delta I_L \text{通常取最大输入电流} I_{in,max} \text{的20\%–40\%}
$$
实际电感范围推荐:
$$
1.2 \cdot L_{min} < L_{actual} < 1.8 \cdot L_{min}
$$
DCM临界条件 (BCM):
$$
L_{crit} = \frac{R D(1-D)^2 T_{sw}}{2} = \frac{V_{in}D(1-D)}{2f_{sw}I_{in}}
$$
4.4 电流路径
| 工作阶段 | 开关状态 | 电流路径 |
|---|---|---|
| 储能阶段 | Q1导通, Q2关断 | Vin → 电感 → Q1 → GND |
| 传输阶段 | Q1关断, Q2导通 | Vin + 电感 → Q2 → (电容+负载) → GND |
| DCM停滞阶段 | Q1关断, Q2关断 | 输出电容 → 负载 → GND |
五、同步Buck-Boost电路解析
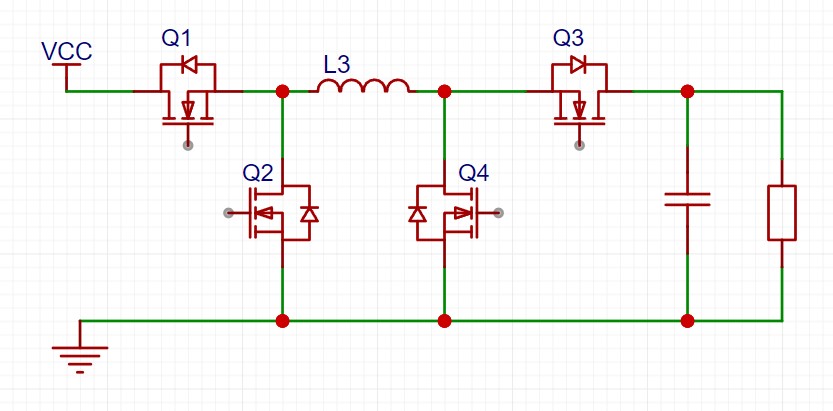
5.1 拓扑结构
通过协调控制4个开关,实现电压的平滑升降
5.2 电压转换特性
纯Buck模式 ($V_{in} > V_{out}$):
- CCM模式 (Q1/Q2进行PWM, Q3常通, Q4常闭):
$$
\frac{V_{out}}{V_{in}} = D
$$
纯Boost模式 ($V_{in} < V_{out}$):
- CCM模式 (Q3/Q4进行PWM, Q1常通, Q2常闭):
$$
\frac{V_{out}}{V_{in}} = \frac{1}{1-D}
$$
过渡模式下的“先降后升”机制 ($V_{in} \approx V_{out}$)
由于 NMOS 自举驱动需要刷新电容,Buck 级无法做到真正的 100% 导通。因此,在输入接近输出时,系统采用“级联补偿”策略,物理过程上确实是先降压、后升压:
- 第一级(Buck 级):先微降
- 为了给自举电容充电,Q1 无法常开,必须以最大占空比(如 95%)工作。
- 后果: 输入电压在经过这一级后,会被强制“砍”掉一小截,导致中间节点电压略低于输入 ($V_{mid} < V_{in}$)。
- 第二级(Boost 级):后微升
- 为了补回 Buck 级造成的电压损失,Boost 级必须以最小占空比(如 5%)介入工作。
- 后果: 将原本偏低的 $V_{mid}$ 重新“抬”起来,使其最终等于输入电压。
5.3 电感参数
电感选型需同时满足Buck和Boost模式的要求,通常分别计算后,取要求更苛刻(即更大)的电感值。
- Buck模式最小电感:
$$
L_{min-buck} = \frac{(V_{in,max}-V_{out}) \cdot V_{out}}{V_{in,max} \cdot \Delta I_L \cdot f_{sw}}
$$ - Boost模式最小电感:
$$
L_{min-boost} = \frac{V_{in,min} \cdot D_{max}}{\Delta I_L \cdot f_{sw}}
$$
最终电感选型:
$$
L_{actual} > \max(L_{min-buck}, L_{min-boost})
$$
5.4 电流路径(重要)
| 工作模式 | 阶段 | 开关状态 | 有效电流路径 |
|---|---|---|---|
| 纯Buck模式 | 电感充电 | Q1导通, Q2关断 Q3常通, Q4常闭 | Vin → Q1 → L → Q3 → 输出 |
| 电感续流 | Q1关断, Q2导通 Q3常通, Q4常闭 | GND → Q2 → L → Q3 → 输出 | |
| 纯Boost模式 | 电感充电 | Q4导通, Q3关断 Q1常通, Q2常闭 | Vin → Q1 → L → Q4 → GND |
| 电感放电 | Q4关断, Q3导通 Q1常通, Q2常闭 | Vin + L → Q3 → 输出 | |
| 过渡模式 | 阶段1 (直通) | Q1, Q3 导通 Q2, Q4 关断 | Vin → Q1 → L → Q3 → GND |
| 阶段2 (补偿) | 交替插入Buck或Boost动作 | ||
| DCM停滞阶段 | (适用于所有模式) | 电感电流为零 所有MOS关断 | 输出电容 → 负载 → GND (电感和开关管无有效电流路径) |