单相全桥逆变器
单相全桥逆变器
|
535

4054 字
|
48 分钟

硬件部分

主功率回路

全桥电路

导通模式

步骤1：初始导通（Q1/Q4导通）

  • 状态：Q1（左上管）与Q4（右下管）导通
  • 电流路径：
    VIN+ → Q1 → 负载上端 → 负载下端 → 电感 → Q4 → VIN-
  • 关键特征：
    • 电感储能阶段（能量来自输入电源）
    • 输出端电压为正向幅值（Vout ≈ Vin）

步骤2：关闭Q1/Q4（换向起点）

关闭顺序：

  • 优先关闭Q1（高压侧管），后关闭Q4（或同步关闭）
  • 死区时间需覆盖最慢关断时间（典型值：100-200ns）

续流路径：

  • 电感电流通过MOS体二极管续流：
    负载下端 → 电感 → Q3体二极管（右上） → VIN+ → VIN- → Q2体二极管（左下） → 负载上端

物理现象：

  • 体二极管导通导致Vds电压降至负值（需注意门极负压防护）

步骤3：死区时间（无开关管导通）

  • 持续时间：50-100ns（由驱动芯片设置）
  • 关键要求：
    • 必须大于最慢体二极管反向恢复时间（推荐SiC MOSFET以缩短死区）
  • 风险控制：
    • 避免共通导通（上下管同时导通导致直通短路）

步骤4：开启Q2/Q3（负半周导通）

  • 导通顺序：同时或略有延迟开启Q2（左下管）和Q3（右上管）
  • 电流转移过程：
    1. 体二极管续流维持电流
    2. MOS沟道逐渐导通，电流从二极管转移到MOS管
  • 稳定路径：
    VIN+ → Q3 → 电感 → 负载下端 → 负载上端 → Q2 → VIN-

步骤5：关闭Q2/Q3（反向换向）

  • 关闭顺序：优先关闭Q3（高压侧管），后关闭Q2
  • 续流路径：
    负载上端 → Q1体二极管 → VIN+ → VIN- → Q4体二极管 → 电感 → 负载下端
  • 关键现象：
    • 电感能量回馈至输入电容（需注意输入电压泵升风险）

步骤6：开启Q1/Q4（新周期开始）

  • 反向恢复影响：
    • Q1/Q4体二极管在导通瞬间产生反向恢复电流尖峰
    • 使用快速恢复二极管或SiC MOSFET可降低尖峰幅度
  • 优化策略：
    • 门极驱动添加米勒钳位电路（抑制Vgs振荡）

输出滤波部分

一、LC滤波 vs LCL滤波对比

特性LC滤波LCL滤波
拓扑结构单电感+单电容双电感+单电容+阻尼网络
适用场景离网逆变、电机驱动并网逆变、高精度电能质量场景
高频衰减-20dB 斜率（低于转折频率）-60dB 斜率（高于谐振点）
谐振风险单谐振峰（需RC阻尼）双谐振峰（必须主动/被动阻尼）
体积/成本电感体积较大总电感量减少30%~50%
EMI抑制有效抑制开关频率谐波可同时抑制高频和低频谐波
关键设计约束避免与负载谐振需精确控制电网阻抗影响

二、LC滤波器参数设计

适用场景：离线式逆变器、UPS、电机驱动（无需并网）

核心设计思想：LC滤波器的主要目标是有效衰减由开关频率 ($f_{sw}$) 产生的纹波，同时确保期望的输出基波频率能够无衰减或低衰减地通过。设计的关键在于将LC滤波器的截止频率 ($f_c$) 设置在远低于开关频率但又显著高于输出基波频率的合理位置。

设计步骤
  1. 确定目标截止频率 ($f_c$)
    滤波器截止频率由L和C共同决定： $$
    f_c = \frac{1}{2\pi\sqrt{L \cdot C}}
    $$ 建议取： $$
    f_c \approx \frac{f_{sw}}{10} \quad \text{（典型取值：1/20 ~ 1/5 }f_{sw}\text{）}
    $$ 示例：若开关频率 $f_{sw}=20\ \text{kHz}$，则取 $f_c \approx 2\ \text{kHz}$
  1. 选择初始元件参数
    根据实际需求选择L或C作为起点：
    • 方法一：优先选定电感L
      $$
      C = \frac{1}{(2\pi f_c)^2 \cdot L}
      $$ 估算电流纹波：
      $$
      \Delta I_L \approx \frac{V_{dc}}{4 \cdot L \cdot f_{sw}}
      $$
    • 方法二：优先选定电容C
      $$
      L = \frac{1}{(2\pi f_c)^2 \cdot C}
      $$
  1. 标称元件选择与验证
    选择最接近标称值后重新计算实际截止频率： $$
    f_{c_actual} = \frac{1}{2\pi\sqrt{L_{nominal} \cdot C_{nominal}}}
    $$ 误差应控制在±10%以内
  1. 纹波验证 验证项目 公式 允许范围 电流纹波 $$\Delta I_L \approx \frac{V_{dc}}{4Lf_{sw}}$$ <20%额定电流峰值 电压纹波 $$\Delta V_{out} \approx \frac{\Delta I_L}{8f_{sw}C}$$ <2%输出电压峰值
  1. 阻尼电阻设计
    抑制谐振峰的推荐参数： $$
    R_{damp} \approx \frac{1}{3}\sqrt{\frac{L}{C}} \quad \text{（与C串联）}
    $$
设计验证案例
案例1：高压逆变器（380V→220VAC）
参数值
直流母线电压380 V
目标截止频率2 kHz
额定功率3 kW
选择电感1.2 mH
计算电容5.28 μF → 选用5.6 μF
实际截止频率1.94 kHz
电流纹波3.96 A (峰值19.3A时20%)
电压纹波4.42 V (峰峰值1.42%)
阻尼电阻4.7 Ω/10W
案例2：低压系统（24V直流输入）
参数值
直流母线电压24 V
目标截止频率2 kHz
已有电感330 μH
计算电容19.19 μF → 18.8 μF实测
实际截止频率2.02 kHz
电流纹波0.91 A (峰峰值)
电压纹波0.30 V (峰峰值1.5%)

三、LCL滤波器参数设计

1. 谐振频率边界设定

$$
10 \cdot \underbrace{f_{grid}}_{\text{电网频率}} < \underbrace{f_{res}}_{\text{谐振频率}} < 0.5 \cdot \underbrace{f_{sw}}_{\text{开关频率}}
$$

  • $f_{grid}$：电网基波频率（50/60Hz）
  • $f_{sw}$：逆变器开关频率（10-50kHz）
  • $f_{res}$：滤波器谐振频率（推荐1-2kHz）
2. 电感参数设计

$$
L_1 \approx \frac{\overbrace{V_{dc}}^{\text{直流电压}}}{k \cdot \underbrace{\Delta I_{L1,pp}}_{\text{纹波峰峰值}} \cdot f_{sw}} \quad \text{（}k=8\text{，SPWM调制系数）}
$$

  • $L_1$：逆变器侧电感（单位：亨/H）
  • $V_{dc}$：直流母线电压（如400V）
  • $\Delta I_{L1,pp}$：允许的纹波电流峰峰值（通常取额定电流的10%-20%）

$$
\begin{cases} L_1 = (60\%\sim70\%)L_{total} \\ L_2 = L_{total} – L_1 \quad \text{（电网侧电感）} \end{cases}
$$

3. 电容参数计算

$$
C = \frac{1}{(2\pi \underbrace{f_{res}}_{\text{目标谐振频率}})^2} \cdot \frac{\overbrace{L_1 + L_2}^{\text{总电感量}}}{L_1 L_2}
$$

  • $C$：滤波电容（单位：法拉/F）
  • $L_1$：逆变器侧电感（0.8mH）
  • $L_2$：电网侧电感（0.45mH）
4. 阻尼网络设计

$$
\underbrace{R_d}_{\text{阻尼电阻}} = \frac{1}{3 \cdot (2\pi f_{res}) \cdot C}
$$

$$
\underbrace{P_{Rd}}_{\text{电阻功率}} = \left( \frac{V_{dc}}{4\sqrt{3}f_{sw}L_1} \right)^2 \cdot R_d \cdot \underbrace{2}_{\text{安全系数}}
$$

  • $R_d$：阻尼电阻（单位：欧姆/Ω）
  • $P_{Rd}$：电阻耗散功率（需满足温升要求）

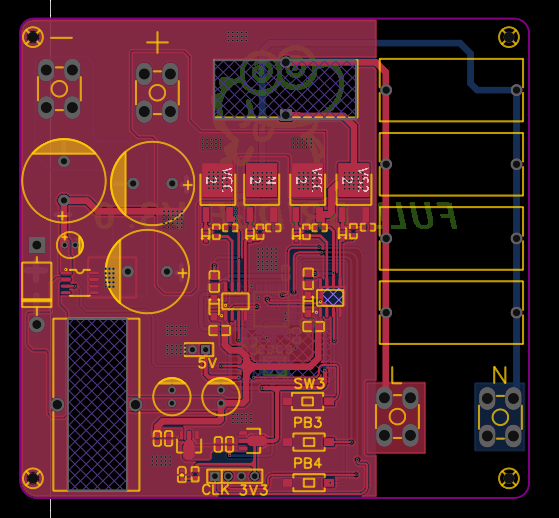
PCB设计

输入→母线电容→全桥MOS管→LC滤波→输出

1. 电容-最短化电流路径

  • 低ESL设计：电容与MOS管构成三角形电流环，寄生电感可压降至<5nH，对比远端布局（如电容放板边）可减少60%电压尖峰
  • 纹波吸收：电容距离MOS管D极<15mm时，高频纹波吸收效率提升3倍（10MHz以上频段）

2. MOS水平阵列

  • 对称性强制：Q1/Q2与Q3/Q4严格镜像对称，各桥臂走线长度偏差<0.5mm（确保导通阻抗一致）
  • 热均衡策略：水平排列使热源均匀分布，配合底部2oz铜箔+散热过孔，温差可控制在ΔT<8℃
  • 开关节点优化：中间两管（Q2/Q3）的D极形成紧凑的SW节点区域，铜箔面积<4cm²（降低辐射EMI）

3. 驱动芯片下置——信号完整性

  • 路径最短化：驱动输出到栅极的路径长度≤20mm，可将栅极回路电感限制在7nH以下
  • 干扰隔离：利用MOS管本体作为天然屏蔽层，驱动电路与功率回路形成垂直电磁隔离

4. LC滤波

  • π型滤波结构：电感前后布置两级电容（例如100μF电解电容+10μF陶瓷电容）
  • 高频滤波：电容GND引脚直接连接至电源地层（非通过过孔），可将100MHz以上噪声衰减20dB
  • 安全间距：电感与电容保持≥5mm间距，避免磁场耦合引发损耗
PCB3
PCB4

软件部分

SPWM参数

1. 调制度（Modulation Index, ( m )）

定义：调制波幅值与载波幅值的比值，决定输出电压幅值
公式：
$$
m = \frac{\sqrt{2} \cdot V_{\text{ph}}}{V_{\text{dc}}} \quad (\text{单极性SPWM})
$$

  • $V_{\text{dc}}$：直流母线电压
  • $V_{\text{ph}}$：输出相电压有效值

取值范围：
$$
0.8 < m < 0.95 \quad \text{(常规逆变器)}
$$

2. 周内点数（Points per Cycle, ( N )）

定义：每个正弦波周期内的PWM脉冲数
公式：
$$
N = \frac{f_{\text{c}}}{f_{\text{m}}} = \frac{T_{\text{m}}}{T_{\text{c}}}
$$

  • $f_{\text{c}}$：载波频率（边缘对齐模式下PWM频率）（单位：Hz）
  • $f_{\text{m}}$：调制波频率（正弦波基波频率）（单位：Hz）

设计规则：
$$
N \geq \begin{cases}
21 & (\text{THD}<5\%) \
81 \sim 201 & (\text{高精度模式})
\end{cases}
$$

3. SPWM中值（Mid-value）

定义：正弦波零点对应占空比
公式：
$$
Mid = \frac{ARR}{2}
$$

4. SPWM幅值（Amplitude of Modulation Wave, ( $V_{\text{m}}$ )）

定义：SPWM峰峰值
公式：
$$
Amp = Mid \times M
$$

5. 载波频率 ($f_c$) 设计规范

设计约束条件：

采样定理约束
$$
f_c \geq 10 \times f_{max}
$$

  • $f_{max}$：系统需处理的最高谐波频率（通常取基波频率的21次谐波）

行业应用指南：

功率等级推荐$f_c$范围适用器件类型损耗分布特性
<1kW10-20kHzMOSFET驱动损耗占比＞60%
1-10kW5-10kHzIGBT/SiC MOSFET开关损耗占比＞70%
>10kW2-5kHzIGCT/压接式IGBT散热设计主导参数
高频应用50-100kHzGaN HEMT需配合零电压切换技术(ZVS)

案例：3kW光伏逆变器参数

参数计算值选用值验证结果
理论$f_c$18.7 kHz20 kHz通过
栅极驱动功耗3.2 W3.8 W温升Δ8℃
器件开关损耗45 W48 W散热器65℃
总效率影响0.7%0.82%符合EN50530

6. PWM对齐模式

参数边缘对齐模式中心对齐模式
实现复杂度简单（单计数器）复杂（双计数器）
谐波分布集中在$f_{\text{c}}$附近分布在2$f_{\text{c}}$附近
死区影响波形不对称度较高对称性好
适用场景低成本单相逆变器三相电机驱动/光伏逆变器
EMI性能较差较好
开关损耗较高（集中在周期边沿）较低（分散分布）

驱动部分

  • 同一桥臂内部：上下管驱动信号严格互补（理想相位差180°）并必须插入死区时间，以防止桥臂直通。
  • 两桥臂之间：
    • 双极性SPWM：通常由一对互补的SPWM信号（一个主PWM和它的反相信号，均包含死区）分别驱动两个桥臂的上管（或半桥驱动芯片的输入），使得两桥臂的输出电压近似反相。
    • 单极性SPWM：通常由两路独立的、相位错开180°的SPWM信号分别驱动两个桥臂（或其半桥驱动芯片），或者通过更复杂的逻辑使得输出电压呈现三电平特性。

双极性SPWM

1. 电压切换特性

  • 输出电平：H桥输出电压（滤波前）在 $+V_{DC}$ 和 $-V_{DC}$ 之间进行双电平切换
  • 电压跳变幅度：在一个开关周期内，电压变化幅度 $\Delta V$ 可达 $2V_{DC}$

2. LC滤波器特性

  • 电容电流：滤波电容 $C_f$ 上的电流由 $$ I_C = C_f \frac{dV}{dt} $$ 决定
    • 电压变化率 $dV/dt$：在24V系统中 ($\Delta V \approx 48V$)，若开关时间为0.24µs – 0.48µs，则 $dV/dt$ 约为 $$100V/\mu s \sim 200V/\mu s$$
    • 典型电流尖峰：$100nF \times (100V/\mu s \sim 200V/\mu s) = \textbf{10A} \sim \textbf{20A}$

3. 直流电源特性

  • 空载电流（RMS估算）：
    $$ I_{RMS} \approx \frac{2V_{DC}f_{sw}C_f}{\sqrt{3}} $$
    实例：24V系统/20kHz开关频率/1.98µF电容时 $I_{RMS} \approx 1.1A$
  • 风险：实测24V电源电压跌落至10V，电流达到限流点

单极性SPWM

1. 电压切换特性

  • 输出电平：H桥输出电压（滤波前）在 $+V_{DC}$、0V、和 $-V_{DC}$ 之间进行三电平切换
  • 电压跳变幅度：主要跳变幅度 $\Delta V$ 通常为 $V_{DC}$

2. LC滤波器特性

  • 电容电流： $$ I_C = C_f \frac{dV}{dt} $$
    • 电压变化率 $dV/dt$：在24V系统中 ($\Delta V \approx 24V$)，$dV/dt$ 降低50%至 $$50V/\mu s \sim 100V/\mu s$$
    • 典型电流尖峰：$100nF \times (50V/\mu s \sim 100V/\mu s) = \textbf{5A} \sim \textbf{10A}$

3. 直流电源特性

  • 空载电流（RMS估算）：
    $$ I_{RMS} \approx \frac{V_{DC}f_{sw}C_f}{2\sqrt{3}} $$
    实例：相同参数下电流降至 $I_{RMS} \approx 0.28A$
  • 优势：电源电压稳定性提升约3.9倍

关键参数对比

技术指标双极性SPWM单极性SPWM
输出电压电平数2电平 ($+V_{DC}$/$-V_{DC}$)3电平 ($+V_{DC}$/0/$-V_{DC}$)
电压跳变幅度$2V_{DC}$$V_{DC}$
电容电流尖峰10-20A@100nF5-10A@100nF
开关频率利用率1×载波频率2×载波频率
THD(@m=0.9)3.8%1.2%
滤波器体积比基准100%电感体积减少40%
EMI主频分布$f_{sw}$±n$f_m$$2f_{sw}$±n$f_m$
开关器件损耗全桥高频开关半桥高频+半桥工频

参考代码

PWM20KHZ 生成正弦表 开20KHZ中断 产生SPWM

/* USER CODE BEGIN Header */
/**
  ******************************************************************************
  * @file           : main.c
  * @brief          : Main program body
  ******************************************************************************
  * @attention
  *
  * Copyright (c) 2025 STMicroelectronics.
  * All rights reserved.
  *
  * This software is licensed under terms that can be found in the LICENSE file
  * in the root directory of this software component.
  * If no LICENSE file comes with this software, it is provided AS-IS.
  *
  ******************************************************************************
  */
/* USER CODE END Header */
/* Includes ------------------------------------------------------------------*/
#include "main.h"
#include "hrtim.h"
#include "tim.h"
#include "gpio.h"

/* Private includes ----------------------------------------------------------*/
/* USER CODE BEGIN Includes */

/* USER CODE END Includes */

/* Private typedef -----------------------------------------------------------*/
/* USER CODE BEGIN PTD */

/* USER CODE END PTD */

/* Private define ------------------------------------------------------------*/
/* USER CODE BEGIN PD */

/* USER CODE END PD */

/* Private macro -------------------------------------------------------------*/
/* USER CODE BEGIN PM */

/* USER CODE END PM */

/* Private variables ---------------------------------------------------------*/

/* USER CODE BEGIN PV */

#define SINE_TABLE_POINTS 400
#define HRTIM_PERIOD_VALUE 57600 // HRTIM 周期寄存器值 (ARR/PER)
#define SPWM_CENTER_VALUE (HRTIM_PERIOD_VALUE / 2)
#define SPWM_AMPLITUDE_VALUE 24480 // 28800 * 0.85

// 正弦查找表 (400点, m=0.85)
const uint16_t sine_table[SINE_TABLE_POINTS] = {
    28800,29184,29568,29950,30332,30712,31090,31467,31842,32215,32587,32956,33323,33688,34050,34410,
    34767,35121,35472,35820,36164,36505,36842,37176,37506,37832,38154,38472,38786,39095,39400,39700,
    39996,40287,40573,40854,41130,41401,41667,41928,42183,42434,42679,42919,43153,43382,43605,43823,
    44035,44242,44443,44639,44829,45013,45192,45365,45532,45693,45849,45998,46142,46280,46412,46538,
    46658,46772,46880,46982,47078,47168,47252,47330,47402,47468,47528,47582,47630,47672,47708,47738,
    47762,47780,47792,47798,47798,47792,47780,47762,47738,47708,47672,47630,47582,47528,47468,47402,
    47330,47252,47168,47078,46982,46880,46772,46658,46538,46412,46280,46142,45998,45849,45693,45532,
    45365,45192,45013,44829,44639,44443,44242,44035,43823,43605,43382,43153,42919,42679,42434,42183,
    41928,41667,41401,41130,40854,40573,40287,39996,39700,39400,39095,38786,38472,38154,37832,37506,
    37176,36842,36505,36164,35820,35472,35121,34767,34410,34050,33688,33323,32956,32587,32215,31842,
    31467,31090,30712,30332,29950,29568,29184,28800,28416,28032,27650,27268,26888,26510,26133,25758,
    25385,25013,24644,24277,23912,23550,23190,22833,22479,22128,21780,21436,21095,20758,20424,20094,
    19768,19446,19128,18814,18505,18200,17900,17604,17313,17027,16746,16470,16199,15933,15672,15417,
    15166,14921,14681,14447,14218,13995,13777,13565,13358,13157,12961,12771,12587,12408,12235,12068,
    11907,11751,11602,11458,11320,11188,11062,10942,10828,10720,10618,10522,10432,10348,10270,10198,
    10132,10072,10018,9970,9928,9892,9862,9838,9820,9808,9802,9802,9808,9820,9838,9862,
    9892,9928,9970,10018,10072,10132,10198,10270,10348,10432,10522,10618,10720,10828,10942,11062,
    11188,11320,11458,11602,11751,11907,12068,12235,12408,12587,12771,12961,13157,13358,13565,13777,
    13995,14218,14447,14681,14921,15166,15417,15672,15933,16199,16470,16746,17027,17313,17604,17900,
    18200,18505,18814,19128,19446,19768,20094,20424,20758,21095,21436,21780,22128,22479,22833,23190,
    23550,23912,24277,24644,25013,25385,25758,26133,26510,26888,27268,27650,28032,28416
};

volatile uint16_t sine_table_index = 0; // 正弦表当前索引


/* USER CODE END PV */

/* Private function prototypes -----------------------------------------------*/
void SystemClock_Config(void);
/* USER CODE BEGIN PFP */

/* USER CODE END PFP */

/* Private user code ---------------------------------------------------------*/
/* USER CODE BEGIN 0 */

/* USER CODE END 0 */

/**
  * @brief  The application entry point.
  * @retval int
  */
int main(void)
{

  /* USER CODE BEGIN 1 */

  /* USER CODE END 1 */

  /* MCU Configuration--------------------------------------------------------*/

  /* Reset of all peripherals, Initializes the Flash interface and the Systick. */
  HAL_Init();

  /* USER CODE BEGIN Init */

  /* USER CODE END Init */

  /* Configure the system clock */
  SystemClock_Config();

  /* USER CODE BEGIN SysInit */

  /* USER CODE END SysInit */

  /* Initialize all configured peripherals */
  MX_GPIO_Init();
  MX_HRTIM1_Init();
  MX_TIM1_Init();
  /* USER CODE BEGIN 2 */
    HAL_HRTIM_WaveformOutputStart(&hhrtim1, HRTIM_OUTPUT_TA1|HRTIM_OUTPUT_TA2); //通道打开
    HAL_HRTIM_WaveformCountStart(&hhrtim1, HRTIM_TIMERID_TIMER_A); //开启子定时器A
    HAL_TIM_Base_Start_IT(&htim1);
  /* USER CODE END 2 */

  /* Infinite loop */
  /* USER CODE BEGIN WHILE */
  while (1)
  {
    /* USER CODE END WHILE */

    /* USER CODE BEGIN 3 */
  }
  /* USER CODE END 3 */
}

/**
  * @brief System Clock Configuration
  * @retval None
  */
void SystemClock_Config(void)
{
  RCC_OscInitTypeDef RCC_OscInitStruct = {0};
  RCC_ClkInitTypeDef RCC_ClkInitStruct = {0};
  RCC_PeriphCLKInitTypeDef PeriphClkInit = {0};

  /** Initializes the RCC Oscillators according to the specified parameters
  * in the RCC_OscInitTypeDef structure.
  */
  RCC_OscInitStruct.OscillatorType = RCC_OSCILLATORTYPE_HSE;
  RCC_OscInitStruct.HSEState = RCC_HSE_ON;
  RCC_OscInitStruct.HSEPredivValue = RCC_HSE_PREDIV_DIV1;
  RCC_OscInitStruct.HSIState = RCC_HSI_ON;
  RCC_OscInitStruct.PLL.PLLState = RCC_PLL_ON;
  RCC_OscInitStruct.PLL.PLLSource = RCC_PLLSOURCE_HSE;
  RCC_OscInitStruct.PLL.PLLMUL = RCC_PLL_MUL9;
  if (HAL_RCC_OscConfig(&RCC_OscInitStruct) != HAL_OK)
  {
    Error_Handler();
  }

  /** Initializes the CPU, AHB and APB buses clocks
  */
  RCC_ClkInitStruct.ClockType = RCC_CLOCKTYPE_HCLK|RCC_CLOCKTYPE_SYSCLK
                              |RCC_CLOCKTYPE_PCLK1|RCC_CLOCKTYPE_PCLK2;
  RCC_ClkInitStruct.SYSCLKSource = RCC_SYSCLKSOURCE_PLLCLK;
  RCC_ClkInitStruct.AHBCLKDivider = RCC_SYSCLK_DIV1;
  RCC_ClkInitStruct.APB1CLKDivider = RCC_HCLK_DIV2;
  RCC_ClkInitStruct.APB2CLKDivider = RCC_HCLK_DIV1;

  if (HAL_RCC_ClockConfig(&RCC_ClkInitStruct, FLASH_LATENCY_2) != HAL_OK)
  {
    Error_Handler();
  }
  PeriphClkInit.PeriphClockSelection = RCC_PERIPHCLK_HRTIM1|RCC_PERIPHCLK_TIM1;
  PeriphClkInit.Tim1ClockSelection = RCC_TIM1CLK_HCLK;
  PeriphClkInit.Hrtim1ClockSelection = RCC_HRTIM1CLK_PLLCLK;
  if (HAL_RCCEx_PeriphCLKConfig(&PeriphClkInit) != HAL_OK)
  {
    Error_Handler();
  }
}

/* USER CODE BEGIN 4 */
void HAL_TIM_PeriodElapsedCallback(TIM_HandleTypeDef *htim)
{
  if(htim->Instance == TIM1) // 确保是TIM1中断
  {
    uint16_t spwm_val_ta1;
    uint16_t spwm_val_ta2;

    // 1. 从正弦表中获取TA1的当前SPWM比较值
    spwm_val_ta1 = sine_table[sine_table_index];

    // 2. 计算TA2的SPWM比较值 (与TA1相差180度)
    //    公式: val_ta2 = HRTIM_PERIOD_VALUE - val_ta1
    //    这个公式适用于单极性SPWM，其中两个桥臂的调制信号反相。
    //    请确保sine_table中的值始终小于HRTIM_PERIOD_VALUE。
    //    如果spwm_val_ta1可能等于HRTIM_PERIOD_VALUE，则spwm_val_ta2会为0。
    //    如果spwm_val_ta1可能为0，则spwm_val_ta2会等于HRTIM_PERIOD_VALUE。
    //    这通常是期望的行为。
    spwm_val_ta2 = HRTIM_PERIOD_VALUE - spwm_val_ta1;

    // 安全钳位 (可选，但推荐，以防正弦表计算有误或溢出)
    // 你的正弦表设计应该已经保证了值在有效范围内 (例如 0 到 HRTIM_PERIOD_VALUE-1)
    // 如果你的正弦表值可以达到 HRTIM_PERIOD_VALUE，那么这里钳位到 HRTIM_PERIOD_VALUE-1 可能更安全，
    // 以避免占空比为100%或0%时可能出现的非常窄的脉冲或无脉冲的问题，具体取决于你的Set/Reset配置。
    // 但是对于标准的周期置位，比较值复位， HRTIM_PERIOD_VALUE 作为比较值意味着整个周期都是高电平（或低电平，取决于极性）。
    // 0 作为比较值意味着在周期开始时就复位。

    // if (spwm_val_ta1 >= HRTIM_PERIOD_VALUE) spwm_val_ta1 = HRTIM_PERIOD_VALUE -1; // 防止100%占空比问题 (如果需要)
    // if (spwm_val_ta1 == 0) spwm_val_ta1 = 1; // 防止0%占空比问题 (如果需要)

    // if (spwm_val_ta2 >= HRTIM_PERIOD_VALUE) spwm_val_ta2 = HRTIM_PERIOD_VALUE -1;
    // if (spwm_val_ta2 == 0) spwm_val_ta2 = 1;


    // 3. 更新 HRTIM Timer A 的比较寄存器
    //    TA1 由 Compare Unit 1 控制
    __HAL_HRTIM_SETCOMPARE(&hhrtim1, HRTIM_TIMERINDEX_TIMER_A, HRTIM_COMPAREUNIT_1, spwm_val_ta1);
    //    TA2 由 Compare Unit 2 控制
    __HAL_HRTIM_SETCOMPARE(&hhrtim1, HRTIM_TIMERINDEX_TIMER_A, HRTIM_COMPAREUNIT_2, spwm_val_ta2);

    // 4. 移动到正弦表的下一个点
    sine_table_index++;
    if (sine_table_index >= SINE_TABLE_POINTS)
    {
      sine_table_index = 0; // 到达表尾则回绕到表头
    }
  }
}
/* USER CODE END 4 */

/**
  * @brief  This function is executed in case of error occurrence.
  * @retval None
  */
void Error_Handler(void)
{
  /* USER CODE BEGIN Error_Handler_Debug */
  /* User can add his own implementation to report the HAL error return state */
  __disable_irq();
  while (1)
  {
  }
  /* USER CODE END Error_Handler_Debug */
}

#ifdef  USE_FULL_ASSERT
/**
  * @brief  Reports the name of the source file and the source line number
  *         where the assert_param error has occurred.
  * @param  file: pointer to the source file name
  * @param  line: assert_param error line source number
  * @retval None
  */
void assert_failed(uint8_t *file, uint32_t line)
{
  /* USER CODE BEGIN 6 */
  /* User can add his own implementation to report the file name and line number,
     ex: printf("Wrong parameters value: file %s on line %d\r\n", file, line) */
  /* USER CODE END 6 */
}
#endif /* USE_FULL_ASSERT */
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																

							
							
						

																

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇